Daily LeetCode #10

https://leetcode.com/problems/split-a-string-into-the-max-number-of-unique-substrings/description/?envType=daily-question&envId=2024-10-21

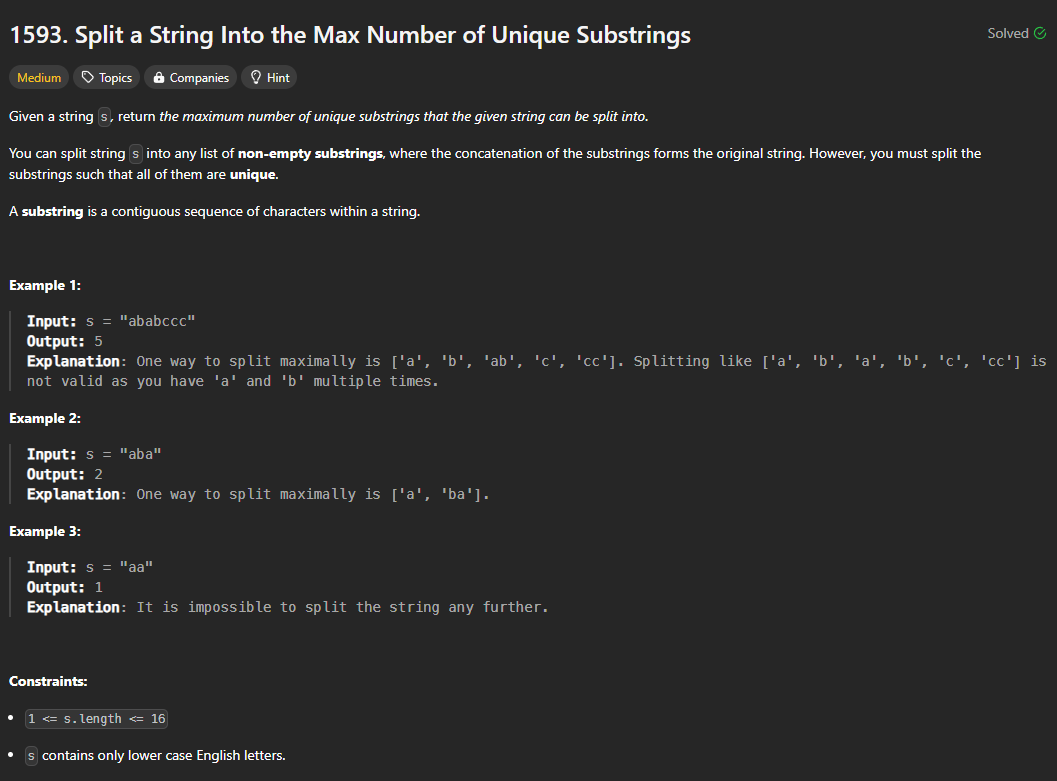
This is a backtrace problem. We check all possbile combinations, and find out the one with most unique substrings.

Steps:

• create a HashMap to store already used substrings
• in the backtrack funtion, we select one substring, check if it is the HashMap
• if already exists, skip this subtstring; else put it into HashMap
• do backtrack recursively with count + 1, since we just select one substring
• whenenver we reach the tree leave, update max
• after finishing checking this subtree, remove the substring and move to the next tree

For example, for s = "aba":

1. select a, put it into HashMap, do backtrack on ba; select b, put it into HashMap; select a, already exists, skip; reach tree node, current max is 2, update max to 2; remove b, select ba, put it into HashMap; reach tree node, current max is 2, no update
2. remove a, select ab, put it into HashMap, do backtrack on a; select a, put it into HashMap; reach tree leave, current max is 2, no update
3. remove ab, select aba, put it into HashMap; reach tree leave, current max is 1, no update

class Solution {

    HashMap <String, Integer> hash = new HashMap<>();
    int max = 0;

    public int maxUniqueSplit(String s) {
        
        backtrack(s, 0, 0);
        return max;
    }

    public void backtrack(String s, int start, int count) {

        // reach tree leave
        if (start == s.length()) {
            max = Math.max(max, count);
            return;
        }


        for(int end = start + 1; end <= s.length(); end++) {
            String curr = s.substring(start, end);
            
            // discard
            if(hash.containsKey(curr)) {
                continue;
            }

            // do selection
            hash.put(curr, 0);

            backtrack(s, end, count+1);
                
            // rollback
            hash.remove(curr);
        }
    }
}

Note:

Since only use HashMap to store existing substrings, the second parameter Integer does not matter.

Time Complexity: O(n 2ⁿ)

[We need to check all possible 2ⁿ combinations, for each combination we use substring, which is O(n)]

Space Complexity: O(n)

https://leetcode.com/problems/kth-largest-sum-in-a-binary-tree/description/?envType=daily-question&envId=2024-10-22

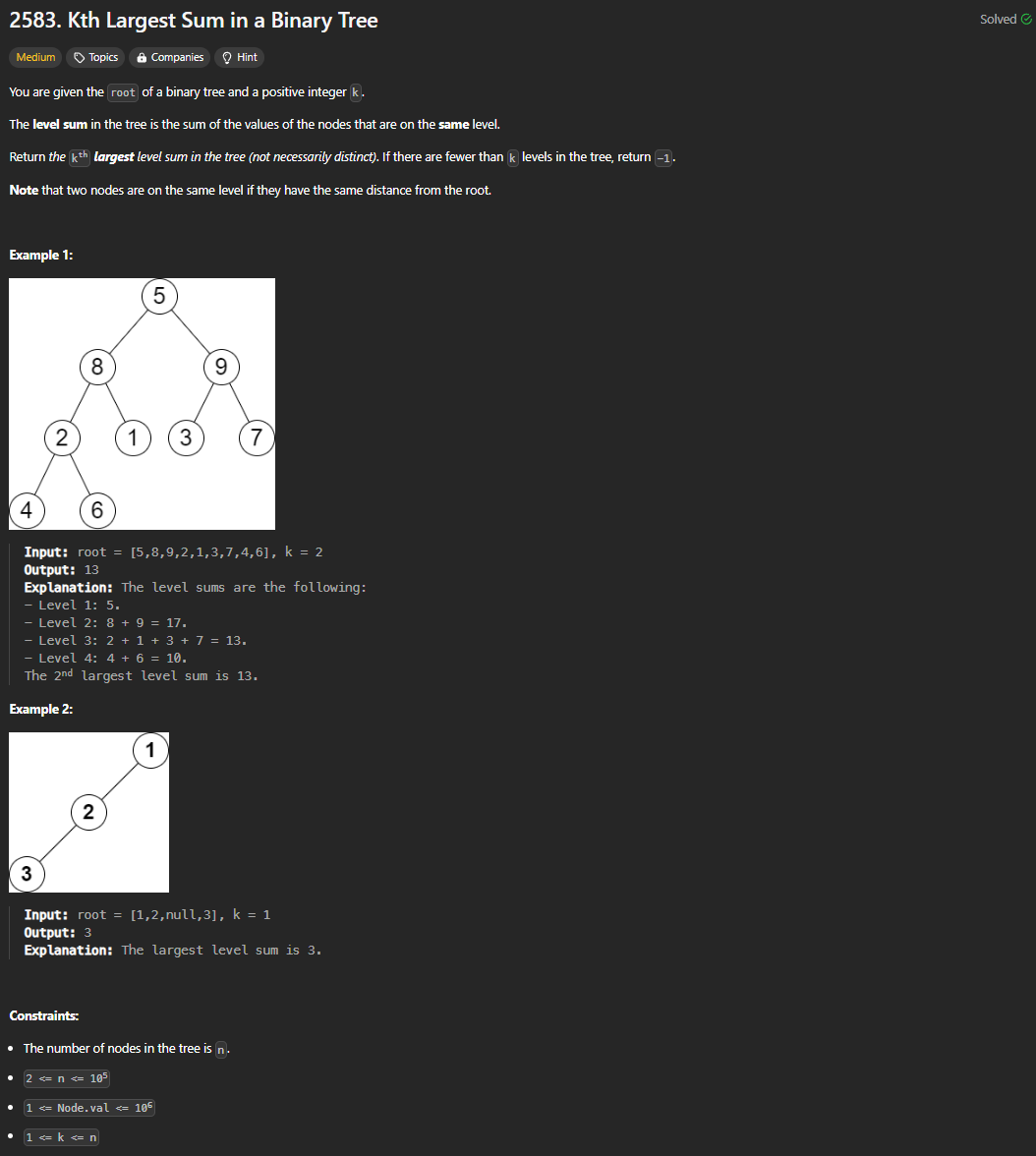
Use BFS to traverse the tree layer by layer.

Steps:

• initialize Queue to start BFS, and a list to store layer sum
• add root into queue
• iterate n time, n is the current size of queue
• after adding node vals, add current node's children into queue
• after each layer, add the layer value sum into the list
• sort the list to get kth largest layer sum

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public long kthLargestLevelSum(TreeNode root, int k) {
        Queue<TreeNode> q = new LinkedList<>();
        List<Long> list = new ArrayList<>();
        // BFS
        q.add(root);

        while(!q.isEmpty()) {
            int size = q.size();
            long sum = 0;
            for(int i = 0; i < size; i++) {
                TreeNode curr = q.poll();
                sum += curr.val;

                if(curr.left != null) q.add(curr.left);
                if(curr.right != null) q.add(curr.right);
            }
            
            // one layer finishes after each for loop
            list.add(sum);
            
        }

        if(k > list.size()) return -1;
        
        // sort
        Collections.sort(list, Collections.reverseOrder());

        return list.get(k - 1);
    }
}

Notes:

Collections.sort(list, Collections.reverseOrder())

sort is from Collections, use reverseOrder() to sort in descending order

Time Complexity: O(nlog(n))

[BFS is O(n); sort is O(nlog(n)) in the worst case that the tree has n layer]

Space Complexity: O(n)

https://leetcode.com/problems/cousins-in-binary-tree-ii/description/?envType=daily-question&envId=2024-10-23

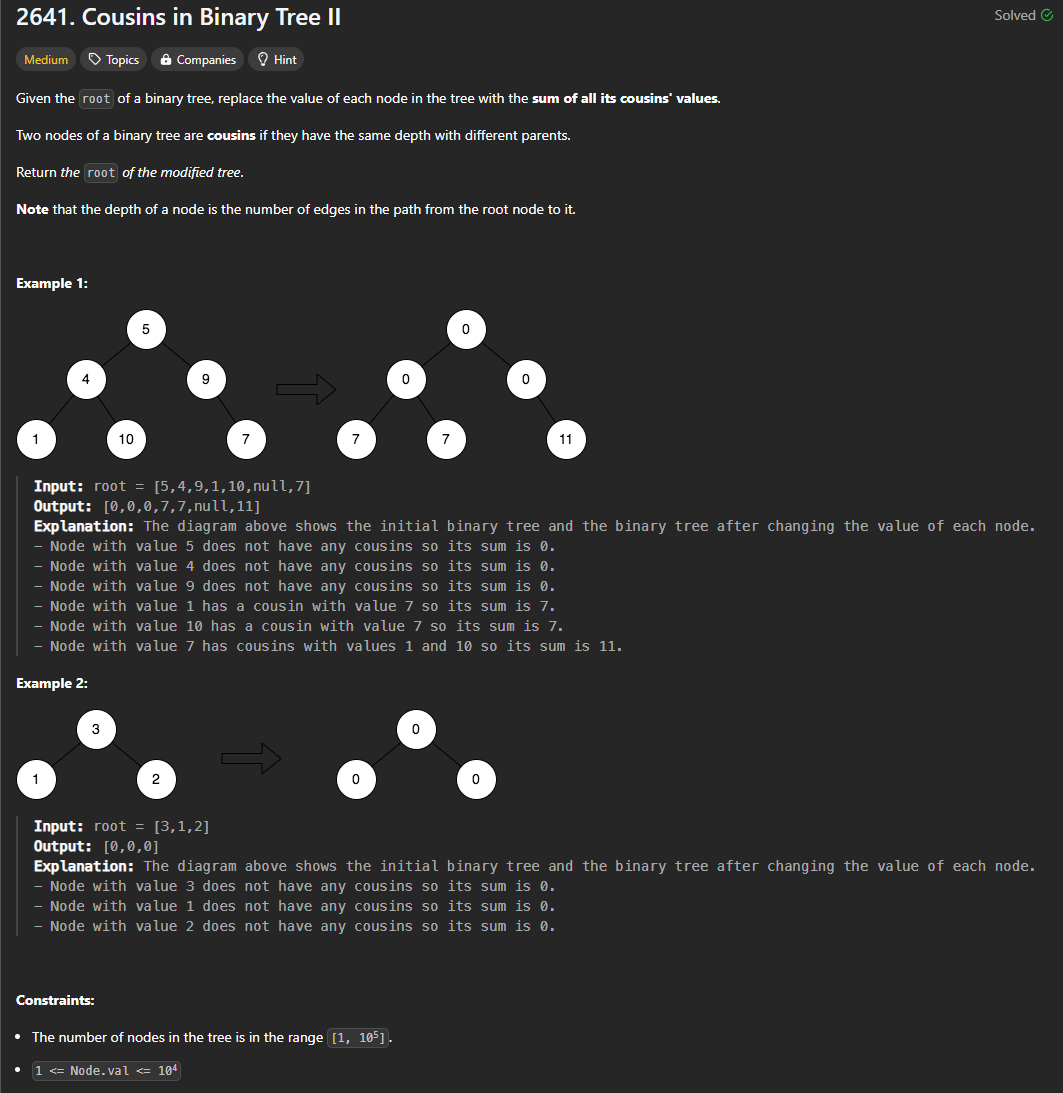
The basic idea is to do BFS twice.

The first BFS is to caculate sum for each layer, and record sibling node for each node.

The second BFS is to update the node val.

Steps:

• the first BFS is almost the same to the last question
• in addition to that, use a HashMap to store <TreeNode, its sibling node's val> to help later calculation
• the second BFS has a integer layer to indicate current layer
• check if current node is top three node, update their val to 0; otherwise, caculate by layerSum - self's val - sibling's val

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode replaceValueInTree(TreeNode root) {
        // queue for BFS
        Queue<TreeNode> q = new LinkedList<>();
        // store sum of each level
        List<Integer> levelSum = new ArrayList<>();
        // store sibling nodes: (node, its sibling node's value)
        HashMap<TreeNode, Integer> hash = new HashMap<>();

        // first time BFS: get levelSum and Sibling info
        q.add(root);

        while(!q.isEmpty()) {
            int size = q.size();
            int currSum = 0;
            
            for(int i = 0; i < size; i++) {
                TreeNode curr = q.poll();
                currSum += curr.val;

                // add sibling value to hash
                if(curr.left != null) {
                  q.add(curr.left); 
                  hash.put(curr.left, (curr.right != null) ? curr.right.val : 0);
                }
                
                if(curr.right != null) {
                  q.add(curr.right); 
                  hash.put(curr.right, (curr.left != null) ? curr.left.val : 0);
                }
            }

            levelSum.add(currSum);
        }

        // second BFS: update node value
        q.add(root);
        
        int level = 0;

        while(!q.isEmpty()) {
            int size = q.size();
            
            for(int i = 0; i < size; i++) {
                TreeNode curr = q.poll();

                // top three nodes
                if(curr == root || curr == root.left || curr == root.right) {
                    curr.val = 0;
                } else {
                    // other nodes
                    curr.val = levelSum.get(level) - curr.val - hash.get(curr);
                }
                
                if(curr.left != null) q.add(curr.left); 
                if(curr.right != null) q.add(curr.right);
            }

            level++;
        }

        return root;
    }
}

Time Complexity: O(n)

[BFS is O(n); HashMap operation is O(1)]

Space Complexity: O(n)