Daily LeetCode #9

https://leetcode.com/problems/parsing-a-boolean-expression/?envType=daily-question&envId=2024-10-20

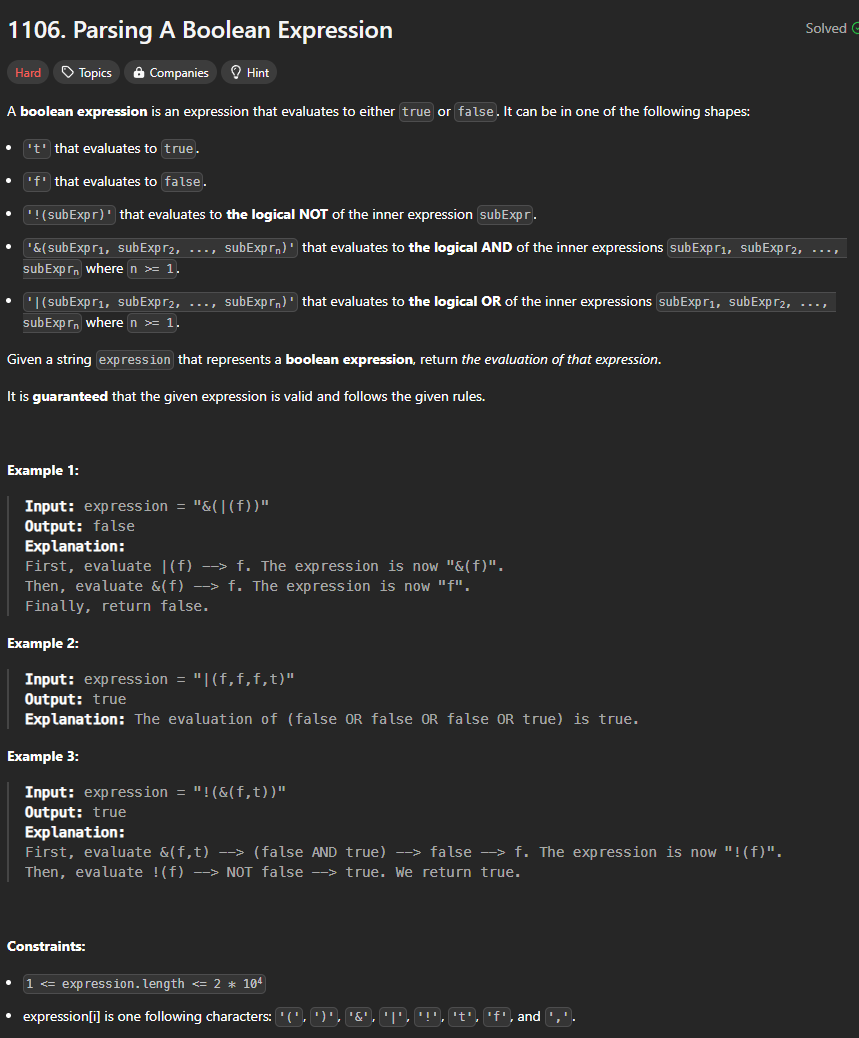
The intuition is to use stack. Then, the problem becomes when to do the operation on f and t, and how to do.

Steps:

• change epression to CharArray
• initialize a stack
• push each char into stack
• if char is ), it means we already have a complete operation that can be caculated
• pop f or t one by one until (, and use f_num and t_num to record the number of f and t
• pop next char, which is (
• pop next char, which is one of |, &, and !
• for |, if t_num > 0, operation result will be t
• for &, if f_num > 0, operation result will be f
• for !, if t_num > 0, operation result will be f
• then push the result into stack again
• after operating all the char, what left in the stack is the result

class Solution {
    public boolean parseBoolExpr(String expression) {
        
        Stack<Character> s = new Stack<>();
        char[] e = expression.toCharArray();
        int f_num = 0;
        int t_num = 0;

        for(char c: e) {
            if(c == ')') {

                // get all the 'f' and 't'
                while(s.peek() != '(') {
                    char d = s.pop();
                    if(d == 'f') {
                        f_num++;
                    } else if(d == 't') {
                        t_num++;
                    } 
                }

                // pop '('
                s.pop();

                // deal with '!', '|', '&'
                char l = s.pop();
                if(l == '|') {
                    s.push((t_num > 0) ? 't' : 'f');
                } else if(l == '&') {
                    s.push((f_num > 0) ? 'f' : 't');
                } else if(l == '!') {
                    s.push((t_num > 0) ? 'f' : 't');
                }

                //intialize f_num and t_num
                f_num = 0;
                t_num = 0;

            } else if(c != ','){
                // push all the others into stack
                s.push(c);
            }
        }

        return s.peek() == 't';
    }
}

Time Complexity: O(n)

Space Complexity: O(n)

https://leetcode.com/problems/find-kth-bit-in-nth-binary-string/?envType=daily-question&envId=2024-10-19

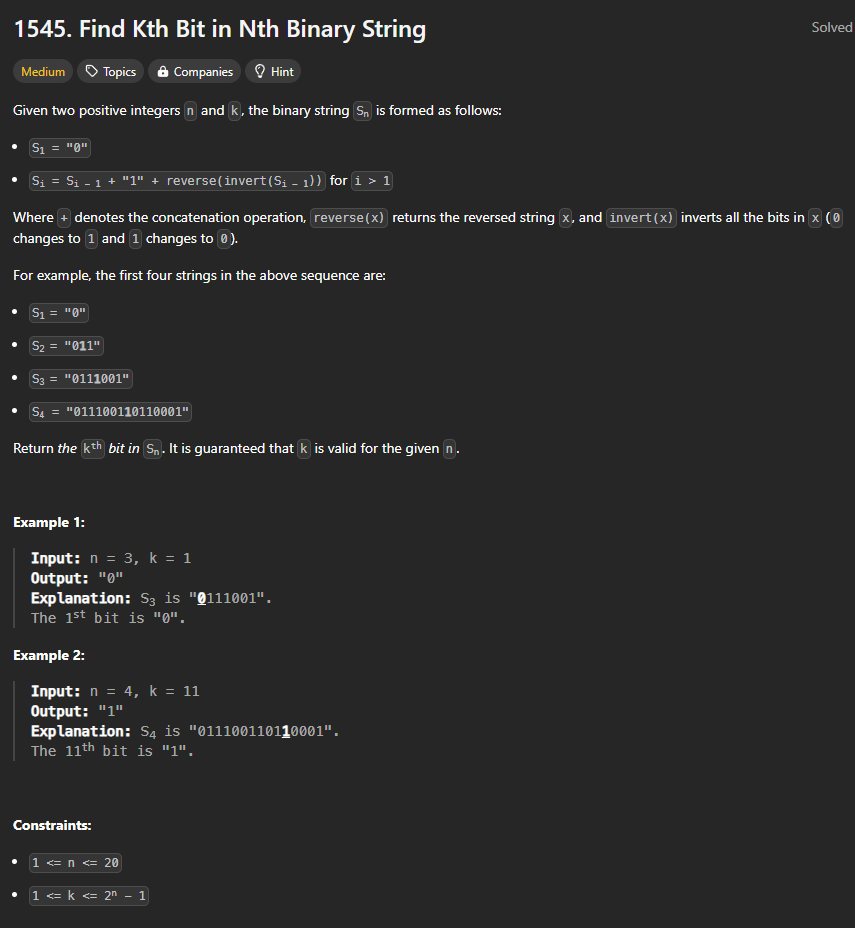
Use recursion and index k as entry points.

Since S_n is contructed by S_n-1, we can use recusion to solve.

Steps:

• the mid index is always 1, so when k is the mid, the result is 1
• if k is less than mid, we go back to S_n-1 for index k
• if k is larger than mid, we also go back to S_n-1 but with reversed index

class Solution {
    public char findKthBit(int n, int k) {
        if(n == 1) return '0';
        
        int l = (1 << n) - 1;
        int mid = l / 2 + 1;

        if(k == mid) {
            return '1';
        } else if(k < mid) {
            return findKthBit(n - 1, k);
        } else {
            return (findKthBit(n - 1, l - k + 1) == '0' ? '1' : '0'); 
        }
    }
}

Notes:

It feels like binary search.

1 << n is equal to 2ⁿ

Time Complexity: O(n)

Space Complexity: O(n)