Daily LeetCode #8

https://leetcode.com/problems/count-number-of-maximum-bitwise-or-subsets/description/?envType=daily-question&envId=2024-10-18

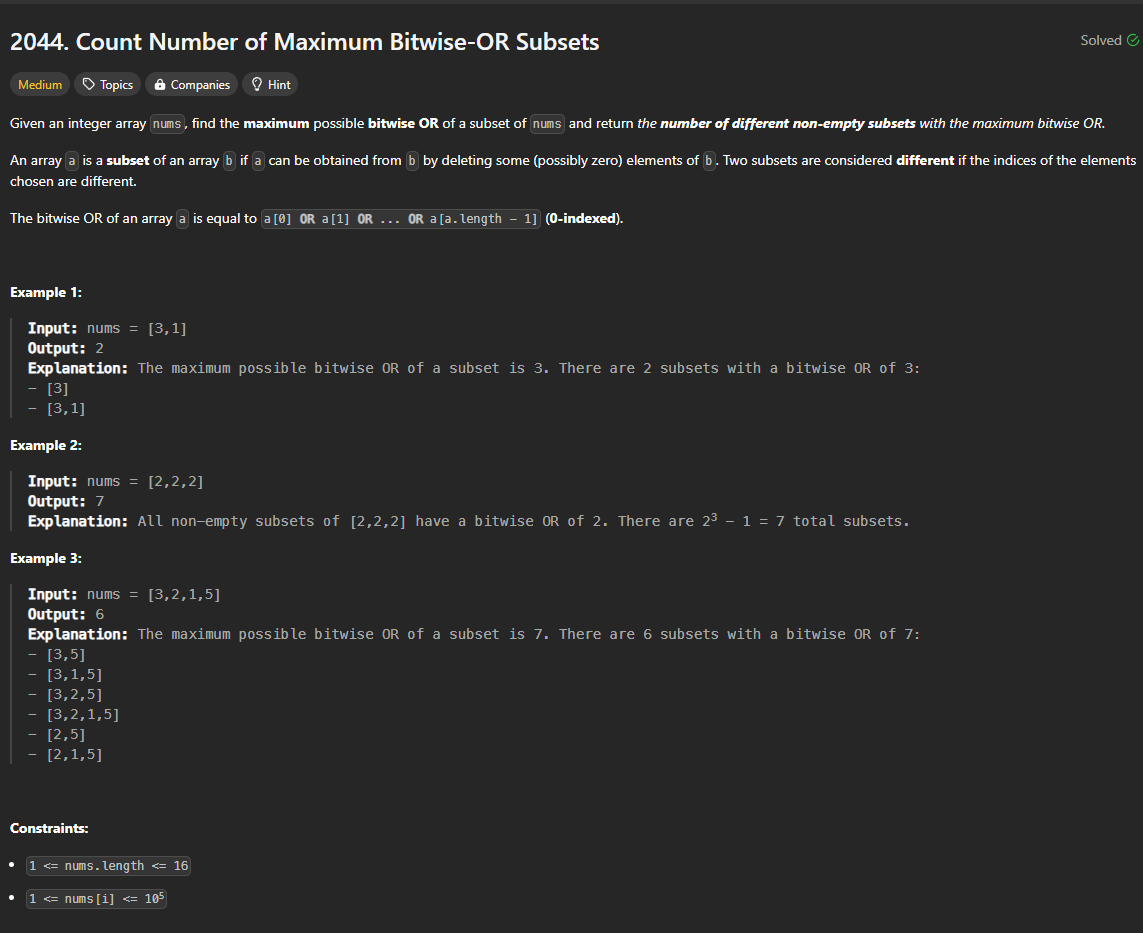
The purpose is to find all the subsets that satisfy: its bitwise OR = max bitwise OR.

Steps:

• the max bitwise OR equals to the bitwise of all the elements in nums
• use a loop to get max, which is max bitwise OR
• enumerate all possible subsets and use count to count valid subsets

class Solution {
    // use global var
    int max = 0;
    int count = 0;

    public int countMaxOrSubsets(int[] nums) {
        // find max
        for(int i = 0; i < nums.length; i++) {
            max |= nums[i];
        }
        
        // list all subsets and check max bitwise OR
        backtrack(nums, 0, 0);

        return count;
        
    }

    public void backtrack(int[] nums, int index, int curr) {
        if(curr == max) {
            count++;
        }

        for(int i = index; i < nums.length; i++) {
            // store original curr
            int prevCurr = curr;
            curr |= nums[i];
            // use i+1 to avoid selecting the same element again
            backtrack(nums, i+1, curr);
            // need to rollback curr
            //eg: finished checking [3] and [3, 1], then to check [1], curr should rollback to 0 
            curr = prevCurr;
        }

    }
}

Use backtrack to enumerate all subsets.

The idea is like a decision tree.

For example, for num = [1, 2, 3].

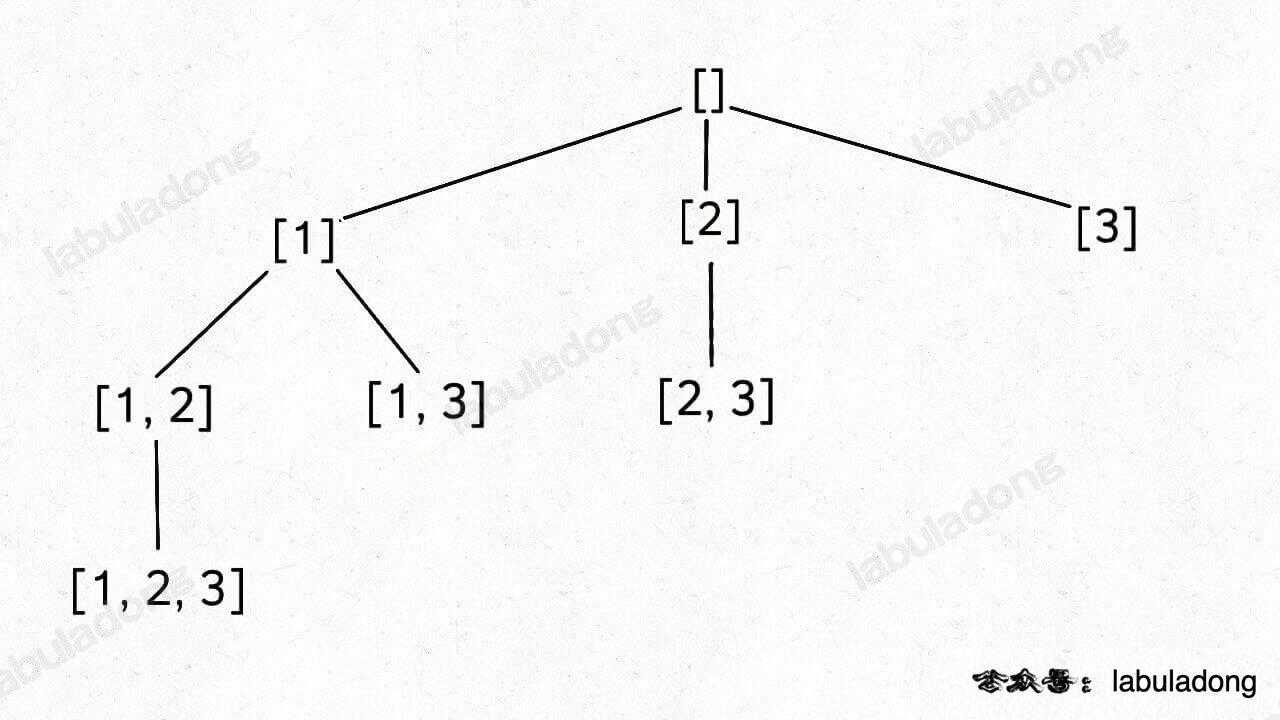
Here we pass parameter i+1 to ensure that the same element is not selected again.

Note: need to rollback curr after returning from the tree leave and entering another subtree from the root. For example, from [1, 2, 3] to [1, 3]; from [1, 3] to [2]; from [2, 3] to [3].

Time complexity: O(n²) [for n elements, the number of subsets is 2ⁿ ]

Space complexity: O(n)

https://leetcode.com/problems/maximum-swap/description/?envType=daily-question&envId=2024-10-17

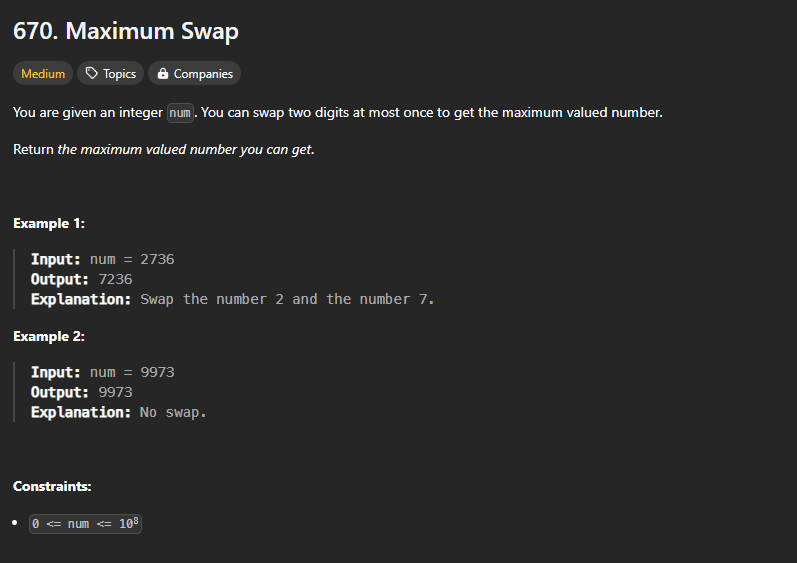
We need to know which numbers should be swap.

For 2376, it is obvious to swap 2 and 7.

For 3176, we swap 3 and 7.

For 3177, we swap 3 and the right most 7.

From those examples, we can see that we always choose the rightest largest digit and leftest digit that is not largest.

We do not choose the smallest digist, since the digit with smaller index is prior in this case.

Steps:

• convert num into CharArray
• for digist 0 to 9, we record the largest index of each and store into an array
• start from left, if we find for a digit, there exist a larger digit on its right side, then it can be swap with the largest digit
• do the swap

class Solution {
    public int maximumSwap(int num) {
        char[] s = Integer.toString(num).toCharArray();
        int n = s.length;
        // use to store largest index of occurance for 0-9 digits
        int[] occur = new int[10];

        for(int i = 0; i < n; i++) {
            int digit = Character.getNumericValue(s[i]);
            occur[digit] = i;
        }

        // find digits to swap
        for(int i = 0; i < n; i++) {
            for(int j = 9; j > Character.getNumericValue(s[i]); j--) {
                if(occur[j] > i) {
                    // swap
                    char temp = s[i];
                    s[i] = s[occur[j]];
                    s[occur[j]] = temp;
                    return Integer.parseInt(new String(s));
                }
            }
        }

        return num;
    }   
}

Notes:

Character.getNumericValue(c) converts character c to corresponding Integer

Integer.parseInt(s) converts String s to a Integer ["1234"[String] -> 1234[int]]

Integer.parseInt(s, n) converts a String representation of radix n to a Integer in radix n. [parseInt("123", 1o) = 123; parseInt("10", 8) = 8]