Daily LeetCode #1

https://leetcode.com/problems/sort-list/description/

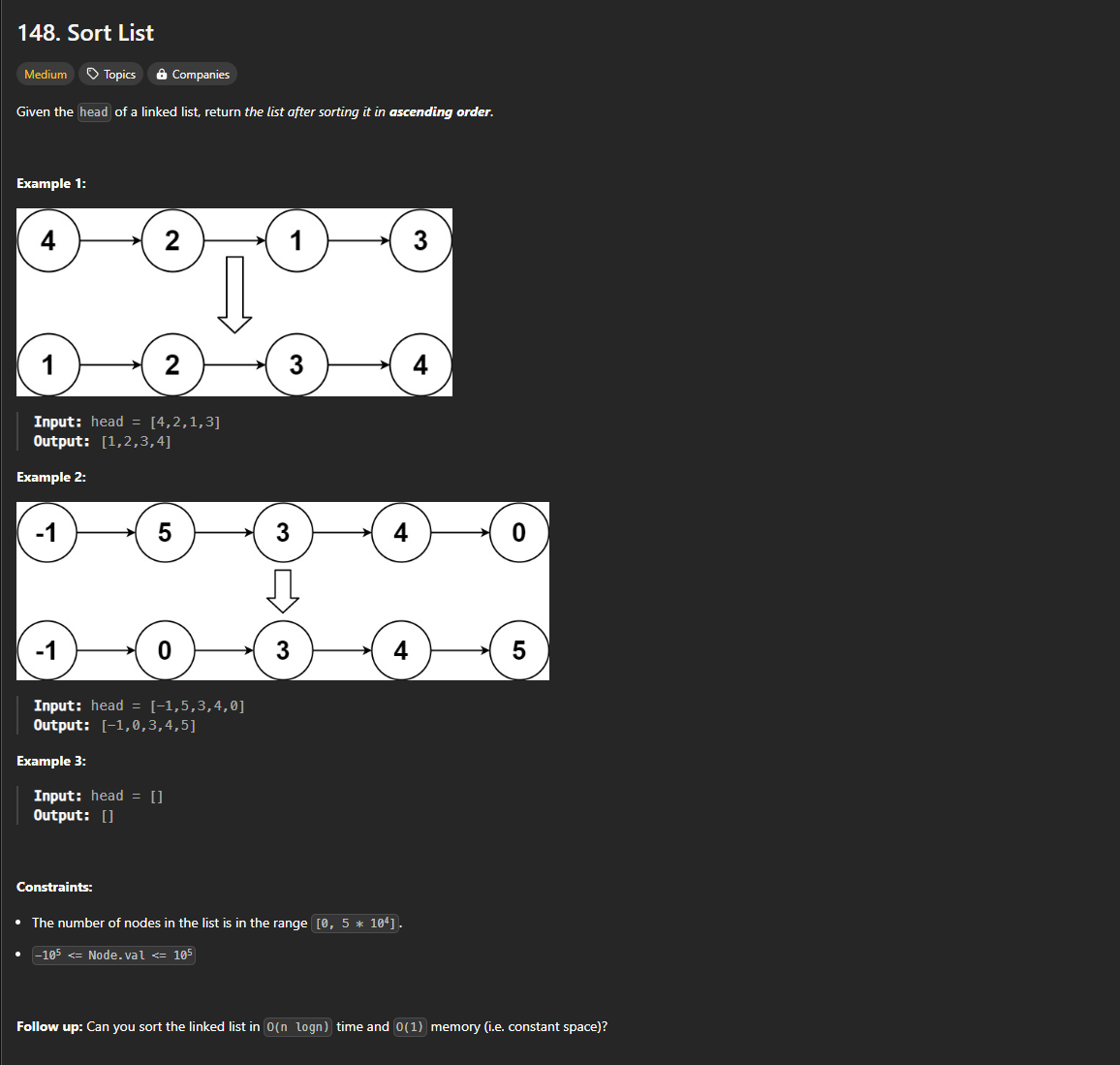
Since time complexity should be O(n logn), consider merge sort or quick sort;

I will use merge sort.

The basic idea of merge sort is:

1. do partition from the mid point recursively
2. do merge and gradually build up the sorted list

Need a function to get the mid node in the linked list, a function to do the merge, and main function to do sort.

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode sortList(ListNode head) {
        if(head == null || head.next == null) return head;
        
        ListNode lastNodeOfLeft = findMid(head);
        ListNode startNodeOfRight = lastNodeOfLeft.next;
        lastNodeOfLeft.next = null;

        // recursion
        ListNode left = sortList(head);
        ListNode right = sortList(startNodeOfRight);
        ListNode res = merge(left, right);
        
        return res;
    }

    ListNode findMid(ListNode head) {
        ListNode fast = head;
        ListNode slow = head;
        // note the conditions have nothing to do with slow pointer
        while(fast.next != null && fast.next.next != null) { 
            slow = slow.next;
            fast = fast.next.next;
        }
        return slow;
    }

    ListNode merge(ListNode a, ListNode b) {
        ListNode dummy = new ListNode(0);
        ListNode trav = dummy;

        while(a != null && b != null) {
            if(a.val < b.val){
                trav.next = a;
                a = a.next;
                trav.next.next = null;
                trav = trav.next;
            } else {
                trav.next = b;
                b = b.next;
                trav.next.next = null;
                trav = trav.next;
            }
        }

        trav.next = (a == null) ? b : a;

        return dummy.next;
    }
}

Funtion findMid() uses fast and slow pointers. Since fast pointer always moves faster, we only need to check its next().

Time Complexity: O(nlogn)

Space Complexity: O(n)

https://leetcode.com/problems/maximum-width-ramp/description/

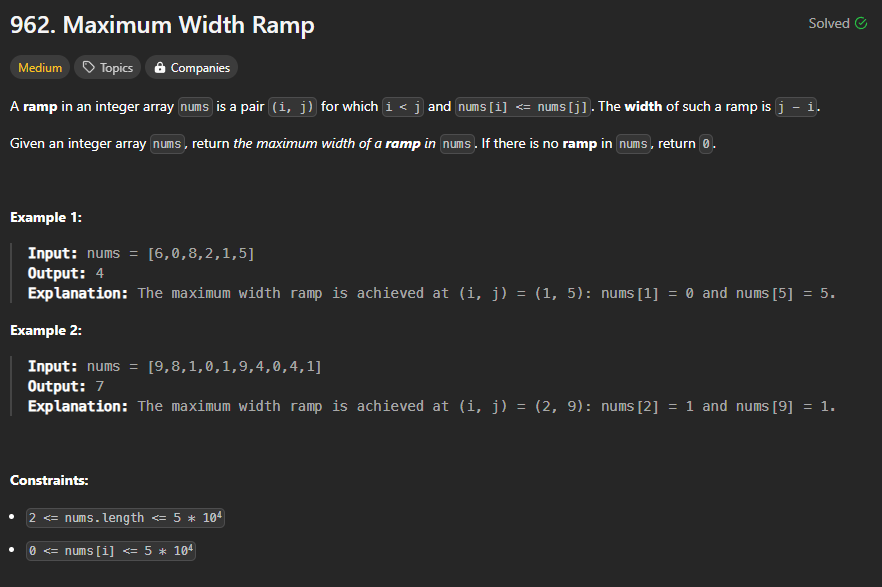
The idea is that the left target i and the right target j should be as far as possible for the distance while the condition nums[i] <= nums[j] works.

i should always be on the left side of j, it feels like a double pointers question.

class Solution {
    public int maxWidthRamp(int[] nums) {
        int res = 0;
        Stack<Integer> stack = new Stack<>();

        for (int i = 0; i < nums.length; i++) {
            if (stack.isEmpty() || nums[i] < nums[stack.peek()]) {
                stack.push(i);
            }
        }

        for (int j = nums.length - 1; j >= 0; j--) {
            while (!stack.isEmpty() && nums[stack.peek()] <= nums[j]) {
                res = Math.max(res, j - stack.pop());
            }
        }

        return res;
    }
}

Use a decreasing stack to store the index starting from left.

Why decreasing?

For example, we have a and b , a is on the left of b and a < b, and we have a j on the right side.
If b < j is true, a < j is also true. Rather than b, we will surely select a as out i, since it is farther from j.
This means that we should prioritize small elements on the left side.

After putting candidates into the stack, use a loop starting from right to get the maximum distance.

Time Complexity: O(n) [only tranvers the list once]

Space Complexity: O(n) [stack will store n elements in the worst case]